
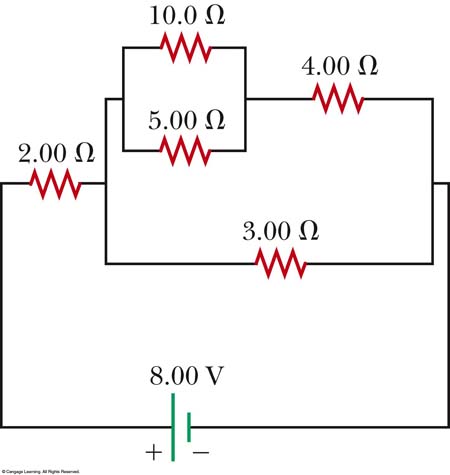
OPENING QUESTIONS: Take a few moments to digest this circuit (If you were here on Thursday be on hot-stand by to assist those of your colleagues who were not):
OBJECTIVE: I will be able to calculate the time constant, instantaneous charge and instantaneous current in an RC circuit after today's class.
WORDS/FORMULAE FOR TODAY
TERMS:
- Time Constant: RC
- Series: occurs when items in a circuit are connected in a line
- Parallel: occurs when items in a circuit
- ElectroMotive Force = EMF= ε=Voltage
- Resistor - an object in an electric circuit which interferes with the flow of electrons through that circuit.
- Drift Speed - The actual speed of motion of electrons in a wire
- Capacitor - two charged surfaces that can store electrical energy
CONSTANTS:
τ = RC (time constant)
UNITS:
- EMF = ε = V
- Power = watts = I2R
- Ohms = resistance = Ω
- (SI Units = ohms)
- breakdown units = volts/ampere
- Capacitance = C
- (SI Units "farads" = F)
FORMULAE:
- ε=IR
- P = I2R
- ∆V = IR
- I = ∆Q/∆t
- I = dq/dt
WORK O' THE DAY:
Calendar issues -
Quiz Tomorrow on:
- Terms, definitions and equations relating to circuit diagrams
- Equivalent Circuits (resistors AND capacitors)
- Kirchoff Rules & Circuit Equations
════════════════════
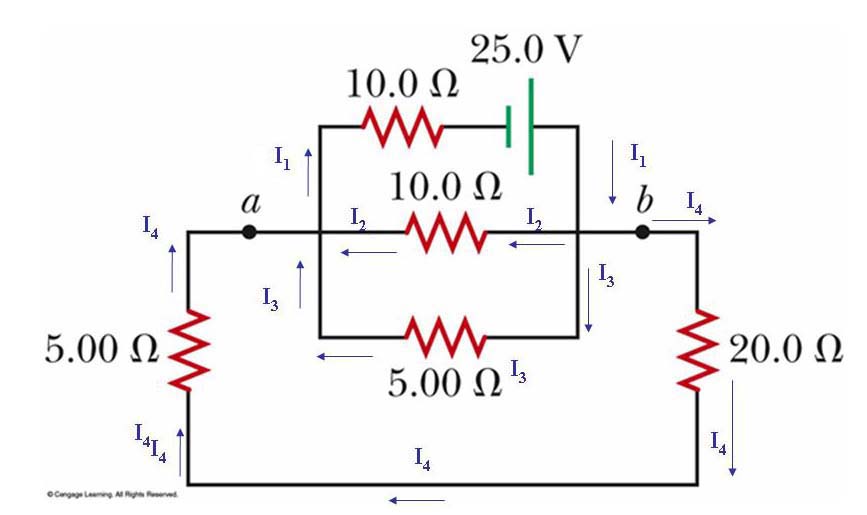
I'll pass this out for your perusal... We're not going to do it all in class, but have a conversation with your groupies and suggest a plan of attack for digesting THIS beastie:
════════════════════
Now let's change gears just a bit and take a gander at what's going on in section 28.4
Take a few moments to recollect what happens as a parallel plate capacitor is charging.
Working with your group please sketch a graph to *suggest* how current changes with time as a capacitor is charging in a simple RC (resistor/capacitor) circuit (that situation occurs when the switch below is set to "a" (I cut off the left side a little too close, there *is* a wire there).

Compare your sketch with THIS:

How did you do? What assumptions or analysis' do you need to change?
Now do the same graph/analysis to suggest what happens to current over time when the capacitor discharges (switch set to "b")
ANSWER:

═════════════════════
Those analysis relate to a common lesson/problem in physics -- mainly how can we take what we know about such an "RC circuit", mainly that the voltage drops across each member in the circuit go to zero:
ε - Q/C - IR = 0
And use that to determine an equation that relates how charge changes over time (and from that, how current changes over time).
The math to do that is a fairly prominent differential equation that we will talk about at LENGTH (see "Charging a Capacitor" begining on page 847) and ending with the equation that relates current over time:
i(t) = (ε/R)e-t/RC
═════════════════════
RC is particularly important so.... like everything in EM that is important we give it a name: Time Constant, and a Greek letter: τ
Similarly, the equation that relates change in current over time to a discharging capacitor is:
i(t) =-(Qi/RC)e-t/RC
════════════════════
Review examples 28.9, 10 & 11
Your TAKEHOME test (15 pts) on this section (28.4) is described in full HERE
Your quiz on section 28.1 - 28.3 is tomorrow as schedule. It will be 30 minutes and involve concepts and homework type problems.